thedeathofall wrote:
I think something is wrong with your math (no offense). That is way to many strokes to be accurate.
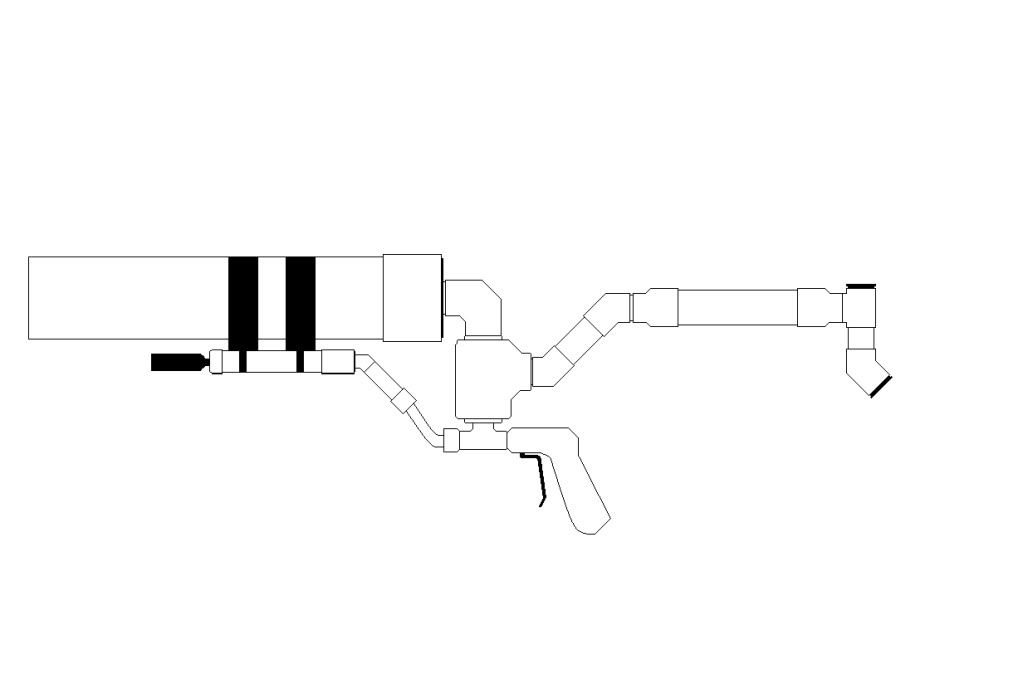
My chamber volume will be around 11.5 cubic inches. The reason why it is so short, is that it will be a built in hand pump for a portable gun. I cant reach out 20 inches.
@ Tech,
So over 86 lbs of force will be required to move it, but how many strokes? how do can that equation be set up?
This will be pumped with one arm. Will this be to hard to use as a built in pump? Should I go with a smaller diameter bore?
Thanks for the input guys!
Veterans, bear with me. I'm trying to keep it simple and in the ballpark. I'm not adding compression heating and expansion to the mix. That is an advanced subject you may wish to learn later.
You need to know a few things at first. 1 is the volume of your pump. You gave a pump cylinder length, but didn't give a stroke length. For this example I'm making the assumption the stroke is the 6.5 inch length given and the cylinder is longer to contain the length of the piston.
Volume of a cylinder is the base area times length.
0.430084034 square inches times 6.5 = 2.795546221 cubic inches.
When compressing gas, it does not care what the pressure on the gauge is. The ABSOLUTE pressure in relation to a vacuum is needed to find the amount of air moved. So we start with 1 atmosphere in the pump which is pushed out on the stroke. Lets call this volume of air 2.795546221 cubic inches at standard temperature and pressure (room temp at atmospheric pressure) Each stroke will deliver this much air in a "Perfect" pump, but alas, there is dead space in the pump at the end of the stroke to the check valve. We will cover that later.
Now on to your chamber. It has a volume and at start it has some air in it at atmospheric pressure. Don't forget it is there even though your gauge reads zero.
To continue the volume of the chamber needs to be known. In the first post this is not given.

For sake of argument assume it is 10 times the volume of the pump. Remember the first amount already in the chamber. Add that pump stroke to it and the chamber which had 10 pump volumes of air now has 11. In 10 strokes it would be at 20 and so forth. So what is the pressure now? Simple take the atmospheric pressure and double it. Using a rounded number of 15 PSI for atmospheric (absolute) that's 30 PSI (absolute). Since the gauge is measuring the relation to the pressure of atmosphere, the gauge will see a difference of 15 PSI.
Working backwards, you want 200 PSI. That's 200 PSI over the 15 PSI atmospheric or a final pressure of 215 PSI absolute.
Pressure is directly related to the volume of the chamber and amount of air pumped in. 10 strokes got us to 15 PSI guage. To make it easier, this pressure is 1 bar. Which is the pressure of the atmosphere doubled or 15 psi. Every 10 strokes gives us 1 bar. We need a total of 13-1/3 bar (200 PSI) so 133 strokes is needed with a perfect pump.
Perfect pump?? yes. Looking at the roughly 13 bar, this is a problem. When we take a stroke and push the plunger all the way down, not all the air goes out. Some remains. How much.. Is it a problem?
Let's assume the space between the piston and check valve and around the piston to the seals is 1/20th the volume of the pump (very believable).
As we pump near the end of pumping up the chamber and near 13 bar, that space has 13X it's volume in that space that doesn't get out of the pump. On the return stroke it returns back to it's original volume as it goes back to 1 atm. That 1/20th of the volume is now 13 times bigger for 13/20ths of the pump volume.
It means at higher pressure you deliver less than 1/2 the volume each stroke so your perfect pump 133 strokes become closer to 300 strokes real world.
A long skinny pump can have a much smaller space because it is skinny and the longer stroke provides a higher ratio of cylinder volume to dead space. This is why shock pumps are long and skinny.
I hope this helps. It is a little long and didn't cover the effects of heating, the force needed to open the check valve, the volume of the hose or pipe to the chamber, moisture condensation, ets. This is a start. :blah5: Why is the math so much work?
As for pumping it one handed, hit the gym and do about 200 reps doing 1 arm curls pulling towards your chest.
The original design is for Popeye or someone working on his biceps to get arms like Popeye.

I used to lift 80 Lb bales of hay. I have a point of reference.
Smaller bore and longer stroke is a really good idea.
Feel free to try the math when you have your pump design and chamber volume figured.