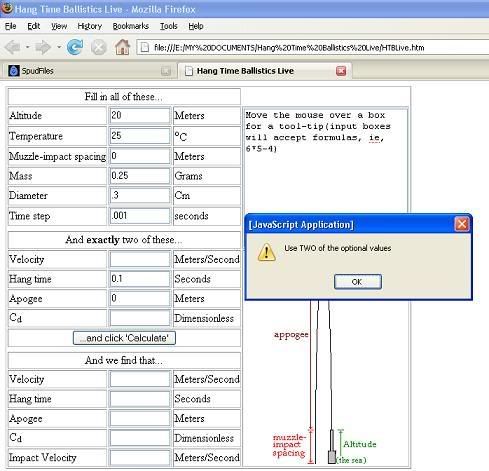
is this a bug or what? I think i entered everything correctly.
EDIT: i found you cannot have zero for the apogee, but what happens if you are shooting from like 1m away? do u put it as 0.0001?








Yep, exactly correct. BTW, if you use the sine then straight up is a 90° launch angle.I simply take the sine of the angle you enter and multiply it by the velocity: this calculates the vertical component of your velocity.
The vertical component of your velocity is then used in the calculations, completely ignoring the horizontal speed.
But it looks like you can fool it buy just entering a very small value, like 0.0001m/s for the muzzle velocity.Yeah, the entered values in the "optional" section have to be above 0... which, as jimmy noted, is because the program doesn't realize you have entered anything if it is zero.




Velocity is a vector quantity so it can be split into two (or more) orthogonal components. I believe it is proper to split the velocity into the vertical and horizontal components before calculating the drag forces, so "Way 2" is the correct method. (See for example https://www.ac.wwu.edu/~vawter/PhysicsN ... ector.html)boilingleadbath wrote:Eh, I'm not so sure that one can model partly-horizontal launches that way. Let's examine a time step in which the projectile is launched at 30* above the horizontal at 100 m/s:
We'll define drag to be equal to (velocity in m/s)<sup>2</sup>
Basically, I cut the constants out of the equation. Still fully functional for this purpose.
Way 1:
(100m/s)<sup>2</sup> = 10,000
sin(30)*10,000 = 5,000 (downward drag units)
Way 2:
sin(30)*100 m/s = 50m/s
(50m/s)<sup>2</sup> = 2,500 (downward drag units)
******************
I expect that "way 1" is the proper way to do it... but the currently implemented system is analogous to the second method.





You need to be a member in order to post a reply
Not a member? register to join our community
Members can start their own topics & subscribe to topics
It’s free and only takes a minute